Summation Notation: What Is It and How to Calculate It?

In mathematics and statistics, the concept of summation notation plays a crucial role in briefly expressing repetitive sums or series. Summation is denoted by the Greek capital letter sigma (∑); summation notation is a powerful tool that simplifies the representation of repetitive sums or series. Understanding its key components and properties allows us to tackle complex mathematical problems with elegance and efficiency. By embracing this concise language of series, mathematicians and researchers can communicate their ideas more effectively and navigate intricate calculations with ease, making summation notation an indispensable asset in the world of mathematics and beyond.

In this article, we will discuss the basics of summation, the concept of summation, the application of summation and the properties of summation. Also, in this article, summation will be explained with the help of detailed examples.

Summation Notation: Concept

Summation notation is a compact mathematical shorthand used to express a sequence of terms to be added together. It is particularly useful when dealing with long sequences or series, as it reduces verbosity and improves readability. The symbol ∑read as “sigma” represents the summation operator and is followed by the term or expression to be summed and the range of values over which the summation is performed.

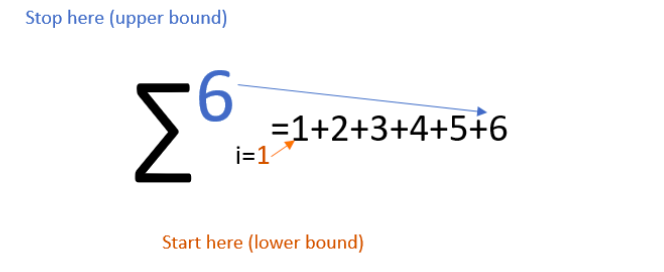
Basics of Summation Notation

• Summation Index: The summation index, represented by a variable or letter (often in lowercase), defines the variable used in the summation expression. It takes on values from a specified range over which the sum is computed.
• Lower and Upper Limits: The lower and upper limits are the bounds of the summation index and determine the starting and ending points for the summation. The main difference between the upper and lower limits only represents the location upper limit written above and the lower limit written below the summation.
• Summand: The summand is the expression to be summed and is written next to the sigma (∑) symbol. It can be a simple variable, a constant, or a more complex mathematical expression involving the summation index.

Summation Notation: Properties 

Summation notation has many properties that simplify and analyze summation notation. Here, we discuss some major applications of summation notation.

1. Linearity: Individual summations can be used to express the total of two or more summations. This is how we may express the linearity characteristic.
   ∑ n k=1 [a(k)+b(k)] = ∑ n k=1 (a(k))+ ∑ n k=1 (b(k))
2. Distributive Property:
   The distributive property of summation can be written in this form
   ∑ n k=1 [c× a(k)]
   And perform that, we take out the value of the constant in summation
   ∑ n k=1 [c× a(k)] =c×∑ n k=1 (a(k))

Applications of Summation Notation

Summation notation is widely used in various fields to analyze and represent mathematical concepts. Here we discuss some major applications of summation notation:

Name	Application
Calculating series	Summation notation is commonly used to represent arithmetic, geometric, and other types of series.For example:The sum of the first n natural numbers: ∑ni=1 (i)= 1 + 2 + 3 + … + n
Calculating definite integrals	In calculus, summation notation can be used to represent the Riemann sum, a method for approximating the definite integral of a function over an interval.
Probability and statistics	Summation notation is widely used in probability and statistics to represent the sum of probabilities or the sum of statistical measures
Discrete mathematics and combinatorics	In combinatorics, summation notation is used to express the number of ways to choose or arrange elements. For representing mathematical relationships in number theory.
Engineering and physics	Summation notation is often used in engineering and physics to represent discrete sums of variables, such as when analyzing discrete signals or discrete data points.
Financial Mathematics	In finance, summation notation can be used to represent the sum of cash flows or to calculate the present value of a series of future cash flows.
Computer science and algorithms	Summation notation is used in algorithm analysis to indicate the temporal complexity of algorithms, the number of operations done by an algorithm function, and the input size.
Signal processing	In signal processing, summation notation is used to represent discrete-time signals and perform various operations on them.

It provides a compact and elegant way to represent repetitive calculations and has widespread utility in mathematics and its applications.

How to simplify a function given in summation form? 

Simplifying a function given in summation form generally involves a few steps. Here’s a general procedure:

1. Understand the Notation: 

Before you can simplify anything, ensure that you understand the summation notation and its components.

2. Expand the Summation (if possible and necessary): 

If feasible, write out the terms explicitly to get a clearer view.

3. Look for Simplifications: 

Combine or cancel out terms as necessary.

4. Apply Properties: 

Utilize properties of summation to simplify the expression further.

5. Evaluate the Sum (if possible): 

For some summations, manual evaluation might be straightforward.

6. Use Known Formulas: 

Familiarize yourself with formulas related to common sequences and series.

1. Use a Summation Calculator:

You can simplify a function given in summation form using online calculators. However, it’s important to choose reliable calculators since not all online tools are accurate. It’s best to use highly recommended summation calculators from reputable math-related websites, such as those offered by AllMath and Icalcualtor.

Example 1:

Solve the following question ∑⁶_x=1(x³-x²+3x-1)

Solution:

 Given question 

∑⁶_x=1(x³-x²+3x-1)                                  (1)

Step 1: Putt all values of x in the given series one by one. 

∑4x=-1(x3-x2+3x-1) =For x=-1	∑4x=-1(x3-x2+3x-1) = (-1)3-(-1)2+3(-1)-1=-1-1-3-1 =-6
∑4x=-1(x3-x2+3x-1) =For x=0	∑4x=-1(x3-x2+3x-1) = (0)3-(0)2+3(0)-1  ∑4x=-1(x3-x2+3x-1)    =0-0+0-1    ∑4x=-1(x3-x2+3x-1)   =-1
∑4x=-1(x3-x2+3x-1) =For x=1	∑4x=-1(x3-x2+3x-1) = (1)3-(1)2+3(1)-1∑4x=-1(x3-x2+3x-1) =1-1+3-1∑4x=-1(x3-x2+3x-1) =2
∑4x=-1(x3-x2+3x-1) =For x=2	∑4x=-1(x3-x2+3x-1) = (2)3-(2)2+3(2)-1∑4x=-1(x3-x2+3x-1) =8-4+6-1∑4x=-1(x3-x2+3x-1) =9
∑4x=-1(x3-x2+3x-1) =For x=3	∑4x=-1(x3-x2+3x-1) = (3)3-(3)2+3(3)-1∑4x=-1(x3-x2+3x-1) =27-9+9-1∑4x=-1(x3-x2+3x-1) =26
∑4x=-1(x3-x2+3x-1) =For x=4	∑4x=-1(x3-x2+3x-1) = (4)3-(4)2+3(4)-1∑4x=-1(x3-x2+3x-1) =64-16+12-1∑4x=-1(x3-x2+3x-1) =59

Step 2:

Putt all 1^st step answer values in equation 1:

∑⁶_x=1(x³-x²+3x-1) = -6-1+2+9+26+59   

      ∑⁶_x=1(x³-x²+3x-1) = 89                     

Example 2:

1 to 50 determine the sum of even number lies between 1 to 50.

Solution:

Step 1: The total even number containing 1 to 50 is 25.

n=25

Step 2: To find the sum, we use the following formula.

Formula for even number = n (n + 1) 

25= 25 (25 + 1) = 25 (26) = 650

FAQs